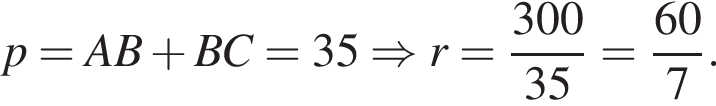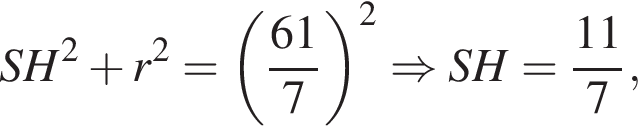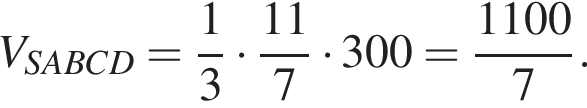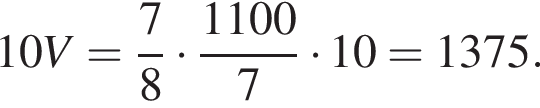Сумма корней (или корень, если он один) уравнения 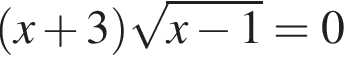 равна:
равна:
Одно число меньше другого на 64, что составляет 16% большего числа. Найдите меньшее число.
График уравнения 1,8x − 0,6y = a проходит через точку А(−2; 9). Найдите число a.
Точка С делит отрезок АВ в отношении 5 : 3, считая от точки А. Если длина отрезка АВ равна 24, то длина отрезка СВ равна:
Найдите значение выражения 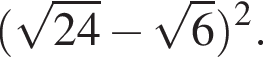
Решением неравенства
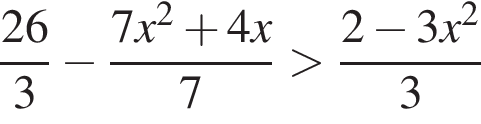
является промежуток:
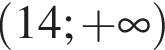 ;
;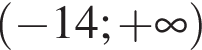 ;
;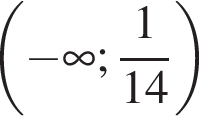 ;
;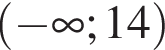 ;
;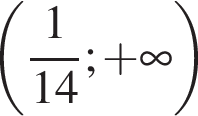 .
.На сторонах квадрата площадью 25 отметили отрезки длиной x. Составьте выражение для определения площади заштрихованной фигуры.
Диаметр окружности пересекает хорду под углом 60° и точкой пересечения делит ее на отрезки длиной 2 и 12. Найдите квадрат радиуса окружности.
Образующая конуса равна 17, а высота — 8 . Найдите площадь боковой поверхности конуса.
Укажите номера уравнений, равносильных уравнению 
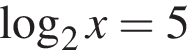
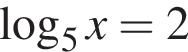
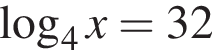
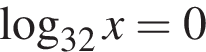
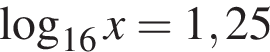
Найдите количество всех целых решений неравенства 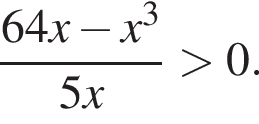
Точки А(1;2), B(5;6) и C(8;6) — вершины трапеции ABCD (AD||BC). Найдите сумму координат точки D, если 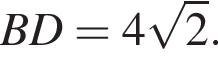
Найдите наибольшее целое решение неравенства 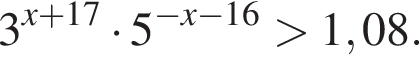
Выберите три верных утверждения:
1) если 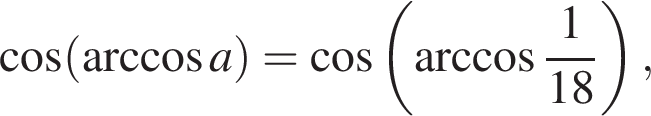 то
то 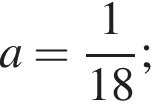
2) если 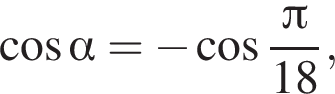 то
то 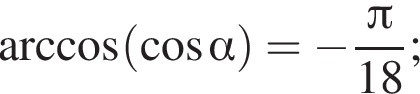
3) если 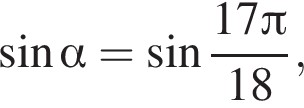 то
то 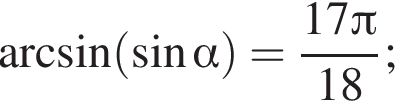
4) если 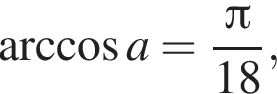 то
то 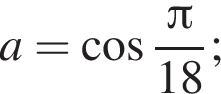
5) если 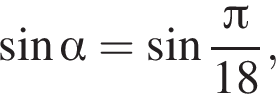 то
то 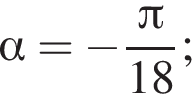
6) если 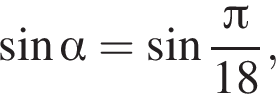 то
то 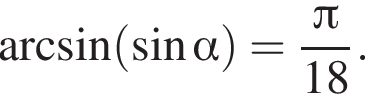
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 123.
Для начала каждого из предложений А−В подберите его окончание 1−6 так, чтобы получилось верное утверждение.
A) Остаток при делении числа 233 на 3 равен ...
Б) Когда карандаши разложили в коробки по 4 штуки в каждую, то получилось 3 полные коробки и осталось 3 карандаша. Количество всех карандашей равно ...
В) Наибольшее натуральное число, которое при делении на 6 с остатком дает неполное частное, равное 2, равно ...
1) 2
2) 1
3) 15
4) 10
5) 17
6) 18
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
На диаграмме показано количество всех покупателей интернет-магазина (П) и количество покупателей, совершивших более одной покупки (ПБ), за период шесть месяцев (с июля по декабрь). Установите соответствие между вопросами А−В и ответами 1−6.
A) В каком месяце количество всех покупателей было наибольшим?
Б) В каком месяце количество покупателей, совершивших более одной покупки, было 160?
В) В каком месяце количество покупателей, совершивших более одной покупки, составило 20% от количества всех покупателей в этом месяце?
1) Июль
2) Август
3) Сентябрь
4) Октябрь
5) Ноябрь
6) Декабрь
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например, А1Б1В4.
В прямоугольном треугольнике ABC
 BH и BK — высота и медиана соответственно, проведенные к гипотенузе (см. рис.). Найдите площадь прямоугольного треугольника ABC, если BK = 7,
BH и BK — высота и медиана соответственно, проведенные к гипотенузе (см. рис.). Найдите площадь прямоугольного треугольника ABC, если BK = 7, 
Четырёхугольник ABCD вписан в окружность. Если 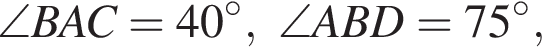 то градусная мера между прямыми AB и CD равна ...
то градусная мера между прямыми AB и CD равна ...
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
Найдите количество корней уравнения 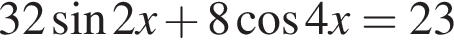 на промежутке
на промежутке 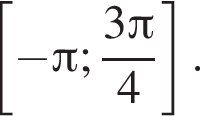
Пусть (x1; y1), (x2; y2) — решения системы уравнений 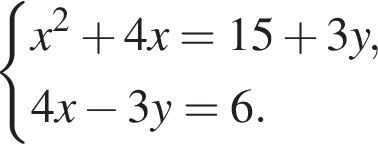
Найдите значение выражения 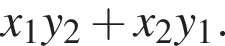
В параллелограмме с острым углом 45° точка пересения диагоналей удалена от прямых, содержащих неравные стороны, на расстояния ![]() и 2. Найдите площадь параллелограмма.
и 2. Найдите площадь параллелограмма.
Найдите увеличенное в 9 раз произведение абсцисс точек пересечения прямой y = 12 и графика нечетной функции, которая определена на множестве  и при x > 0 задается формулой
и при x > 0 задается формулой 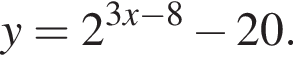
Найдите значение выражения 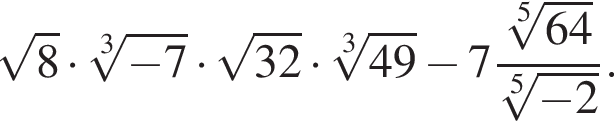
В арифметической прогрессии 130 членов, их сумма равна 130, а сумма членов с четными номерами на 130 больше суммы членов с нечетными номерами. Найдите сотый член этой прогрессии.
Количество целых решений неравенства 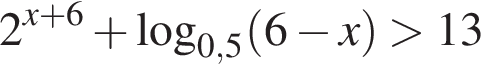 равно ...
равно ...
Если 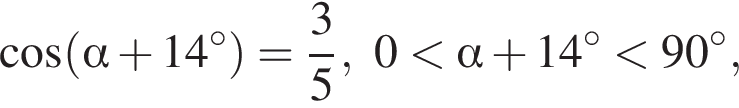 то значение выражения
то значение выражения 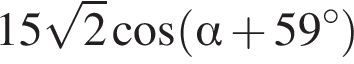 равно ...
равно ...
Пусть 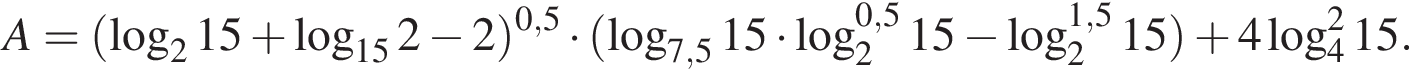
Найдите значение выражения 2A.
Найдите произведение наибольшего целого решения на количество всех натуральных решений неравенства 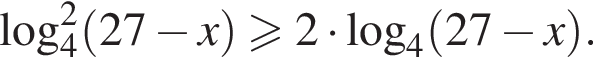
Основанием пирамиды SABCD является выпуклый четырехугольник ABCD, диагонали АС и BD которого перпендикулярны и пересекаются в точке O, АО = 9, ОС = 16, ВО = OD = 12. Вершина S пирамиды SABCD удалена на расстояние ![]() от каждой из прямых AB, BC, СD и AD. Через середину высоты пирамиды SABCD параллельно ее основанию проведена секущая плоскость, которая делит пирамиду на две части. Найдите значение выражения 10 · V, где V — объем большей из частей.
от каждой из прямых AB, BC, СD и AD. Через середину высоты пирамиды SABCD параллельно ее основанию проведена секущая плоскость, которая делит пирамиду на две части. Найдите значение выражения 10 · V, где V — объем большей из частей.

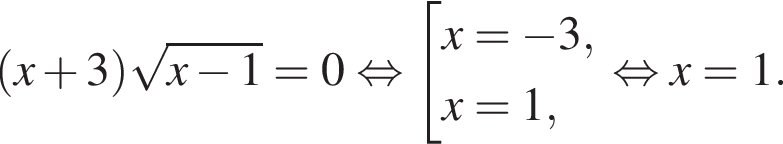
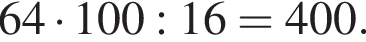 Таким образом, меньшее число
Таким образом, меньшее число 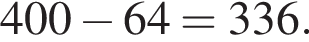
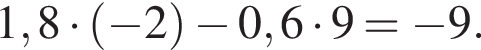
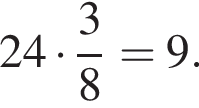
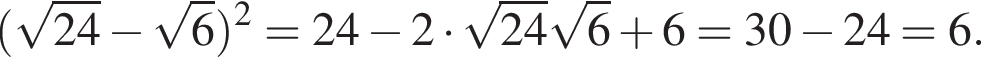
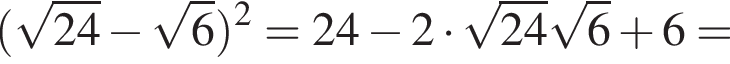
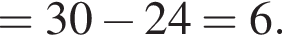
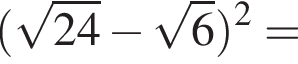

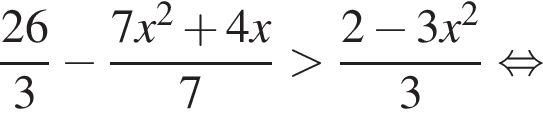
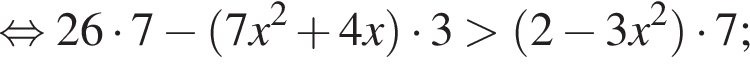
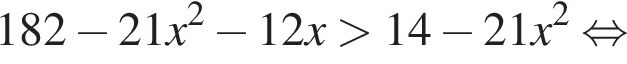

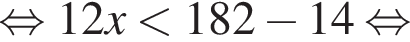

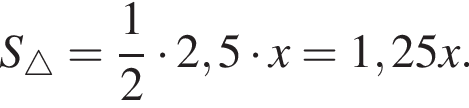
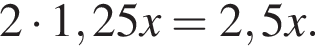 Таким образом, площадь заштрихованной фигуры будет равна
Таким образом, площадь заштрихованной фигуры будет равна 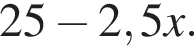

 а значит,
а значит, 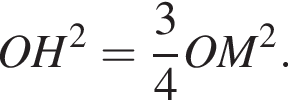 Следовательно,
Следовательно, 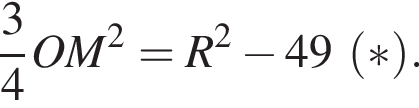
 откуда
откуда  Подставляя в (⁎), получаем:
Подставляя в (⁎), получаем: 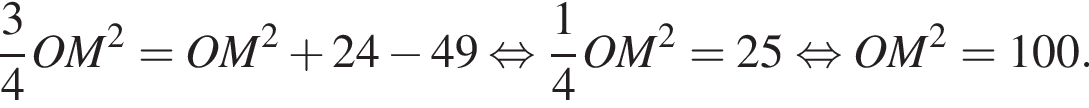
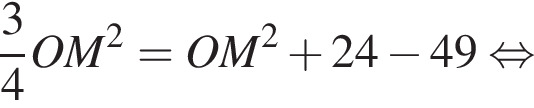
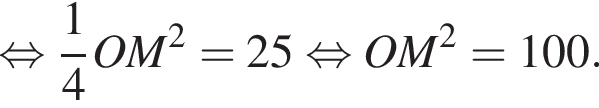
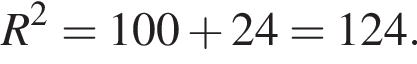
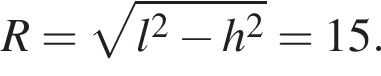
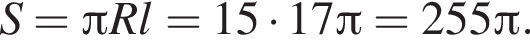
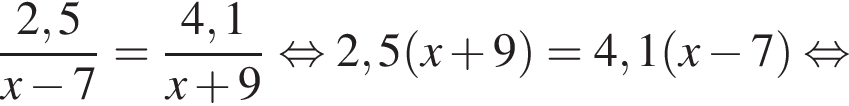
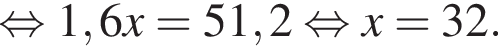
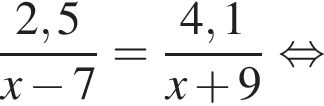

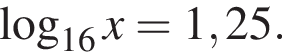
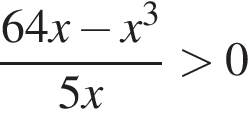
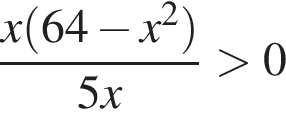
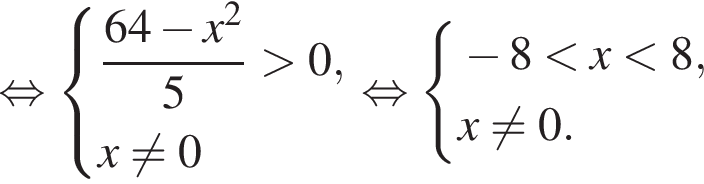
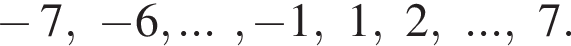
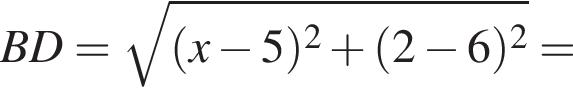
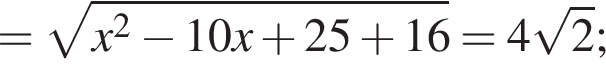
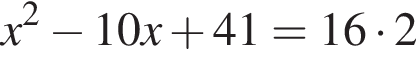
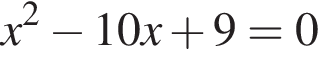
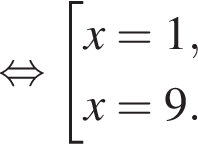
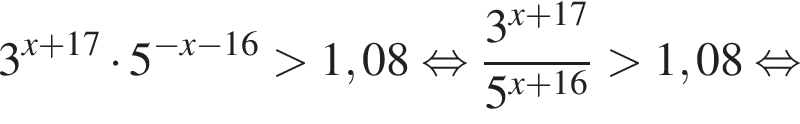
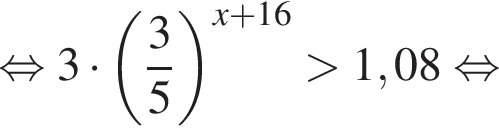
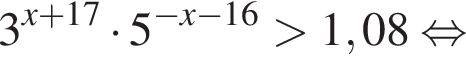
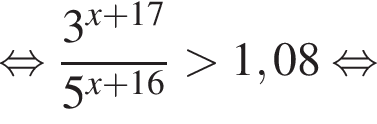
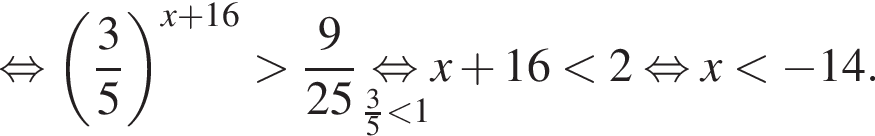
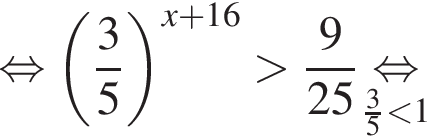
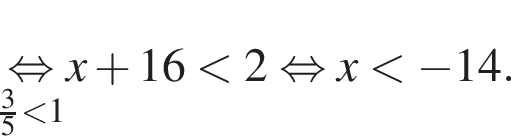
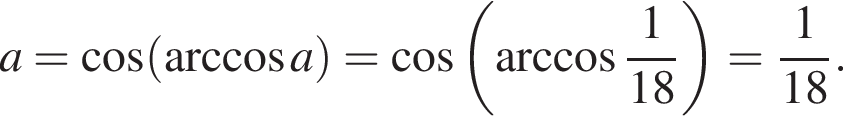

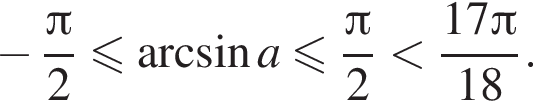
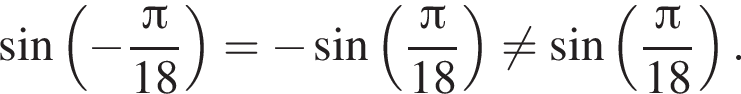
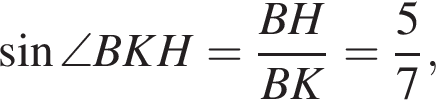 а BK = 7, получаем, что BH = 5. Отрезок BK — медиана прямоугольного треугольника, проведенная к гипотенузе, длина BK равна половине длины гипотенузы, тогда длина гипотенузы равна 2BK = 14. Площадь треугольника ABC равна
а BK = 7, получаем, что BH = 5. Отрезок BK — медиана прямоугольного треугольника, проведенная к гипотенузе, длина BK равна половине длины гипотенузы, тогда длина гипотенузы равна 2BK = 14. Площадь треугольника ABC равна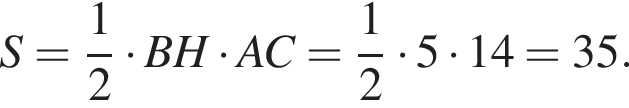



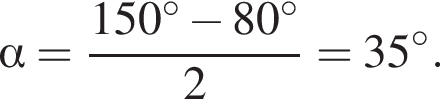
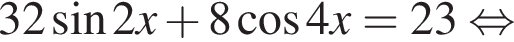
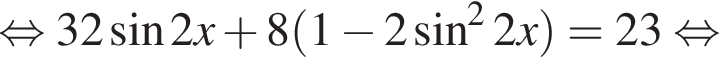
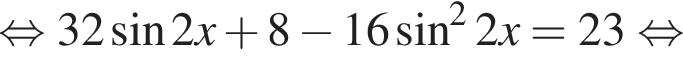
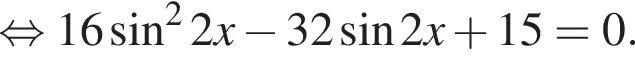
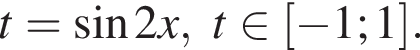 Тогда:
Тогда: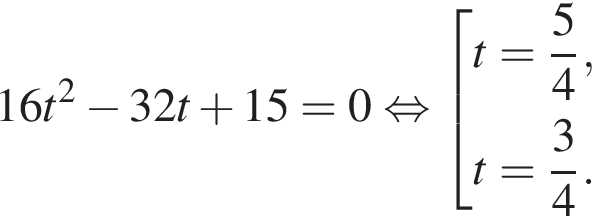
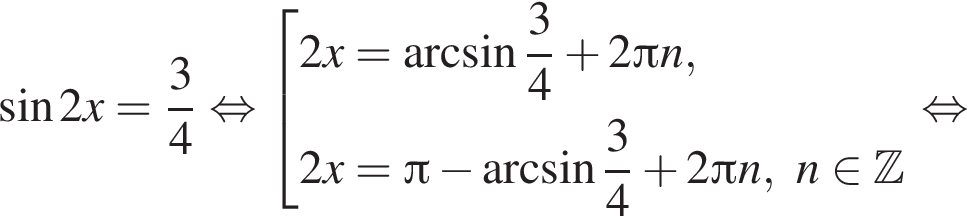
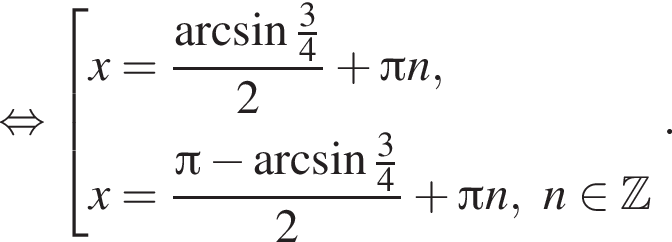
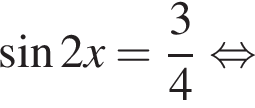
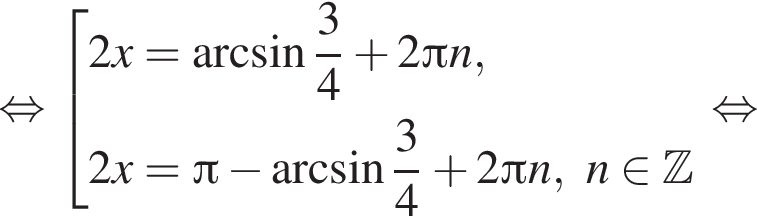
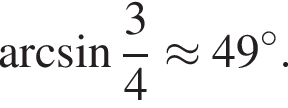 Рассмотрим значения x при различных значениях n:
Рассмотрим значения x при различных значениях n: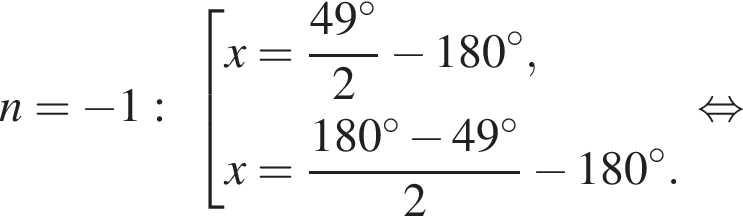
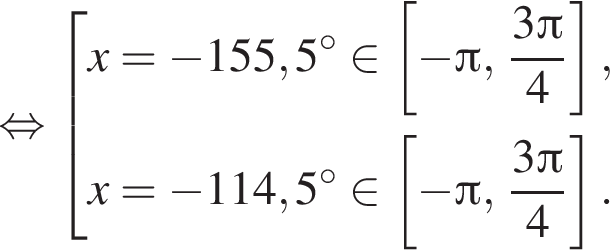
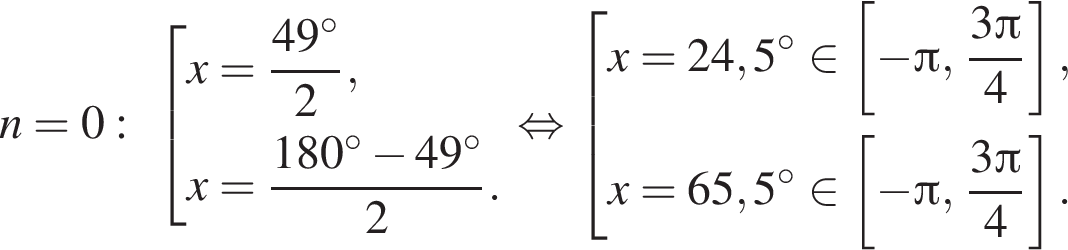
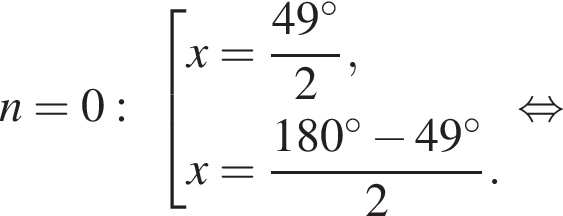
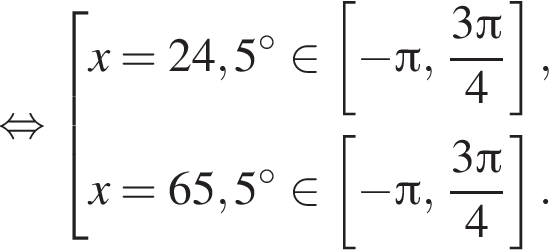

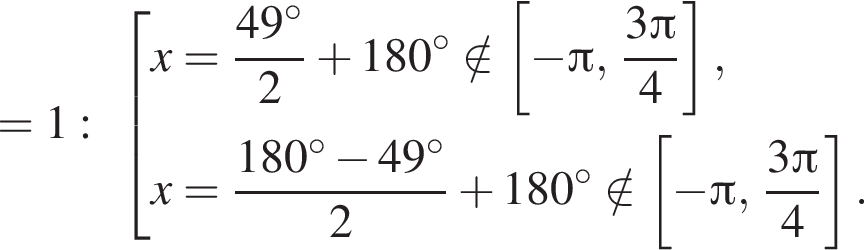
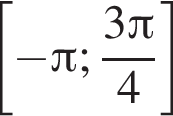 4 корня.
4 корня.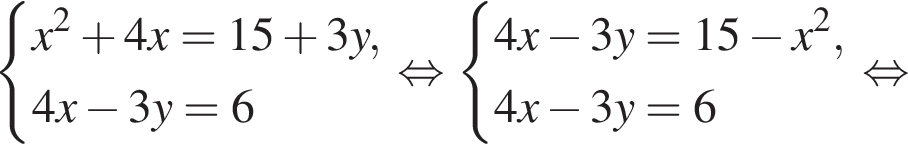
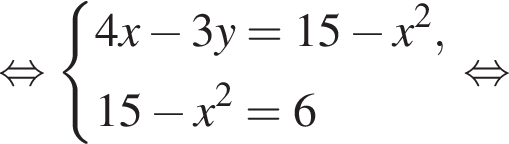
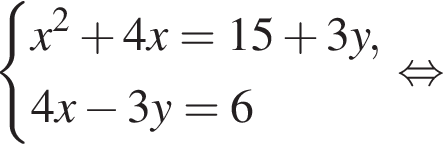
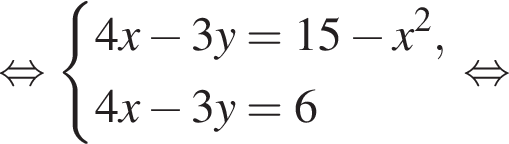
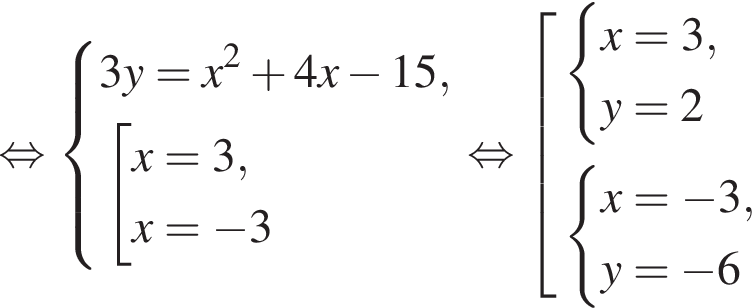

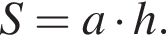 Синус известного угла есть отношение высоты и одной из сторон. Найдем одну из сторон параллелограмма, полагая, что высота равна 2 · 2 = 4:
Синус известного угла есть отношение высоты и одной из сторон. Найдем одну из сторон параллелограмма, полагая, что высота равна 2 · 2 = 4: 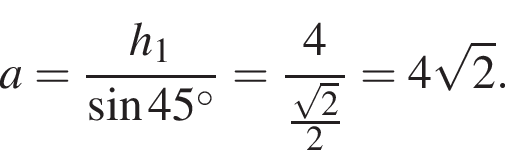 Таким образом, искомая площадь параллелограмма равна произведению найденной стороны на высоту
Таким образом, искомая площадь параллелограмма равна произведению найденной стороны на высоту 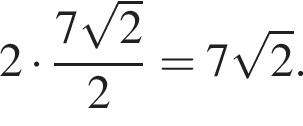
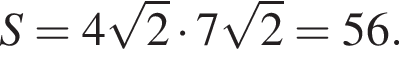

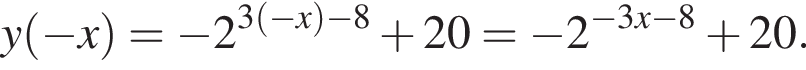
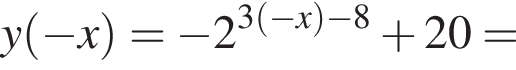
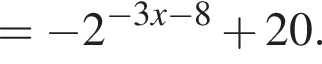
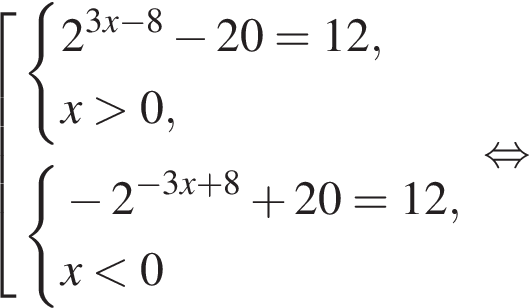
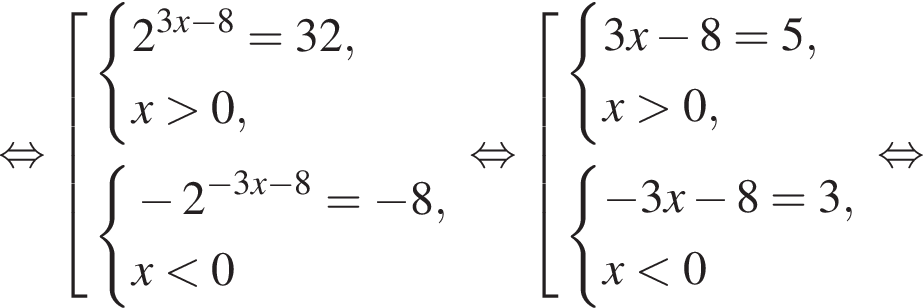
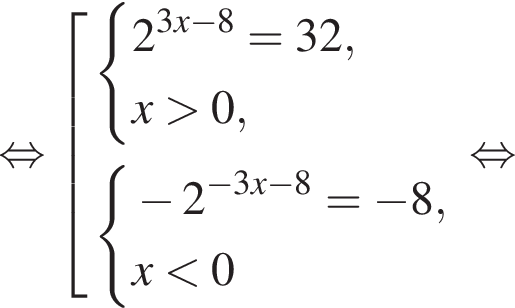
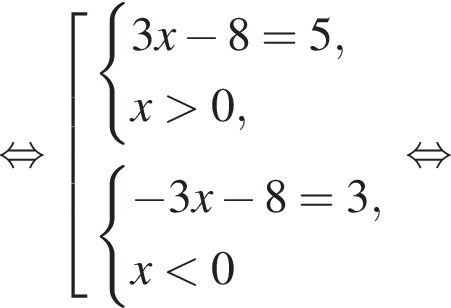
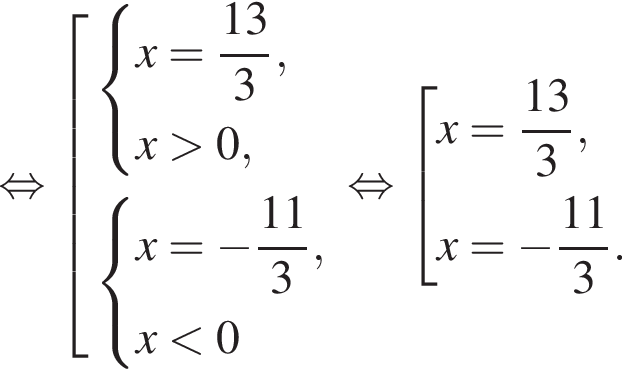
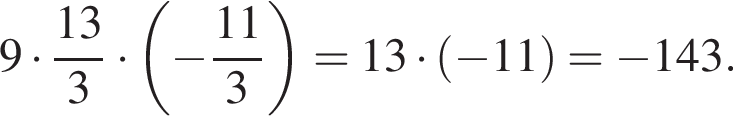
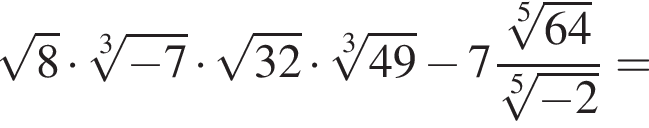
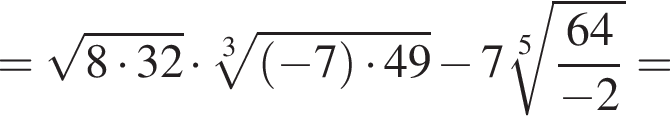
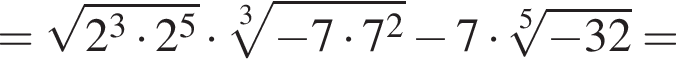
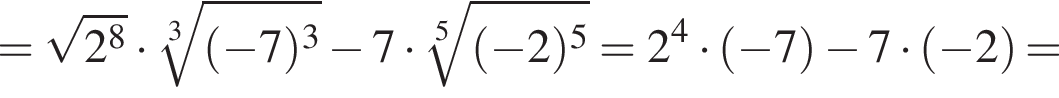
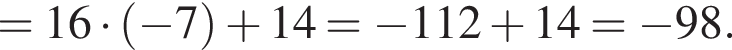
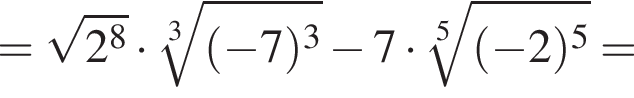
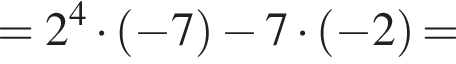
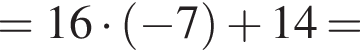

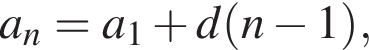 где d — разность арифметической прогрессии.
где d — разность арифметической прогрессии. 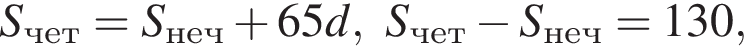 откуда
откуда 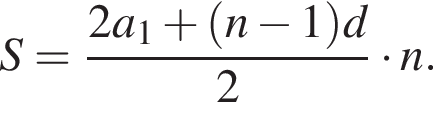 Следовательно, согласно условию, имеем:
Следовательно, согласно условию, имеем: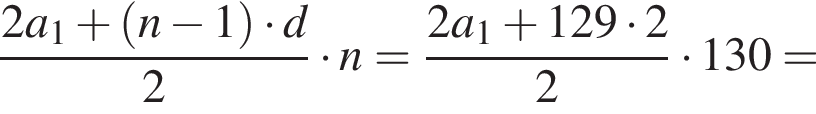
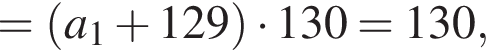
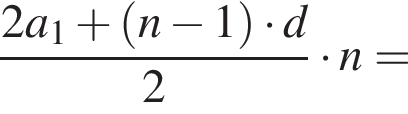
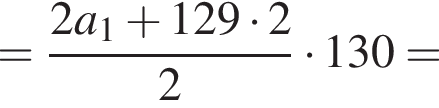
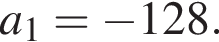 Получим
Получим 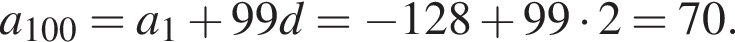
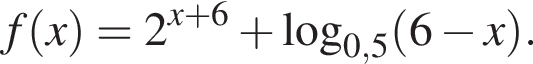 Заметим, что по смыслу задачи
Заметим, что по смыслу задачи 
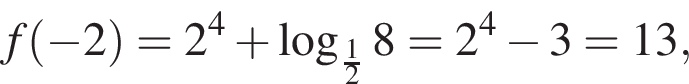 неравенство верно для всех x из
неравенство верно для всех x из 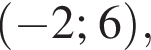 который содержит 7 целых чисел:
который содержит 7 целых чисел: 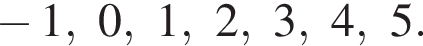
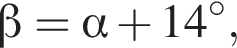 следовательно,
следовательно, 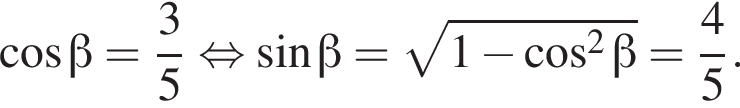 Заметим, что
Заметим, что  Таким образом:
Таким образом: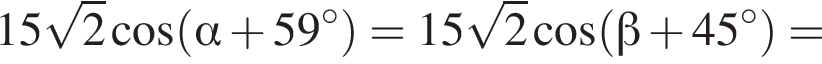
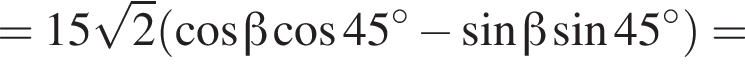
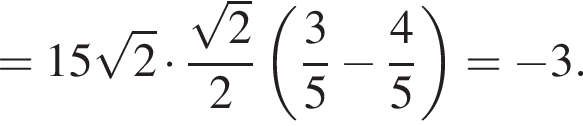
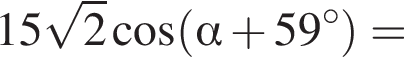
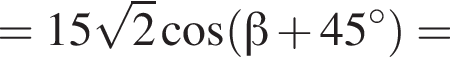

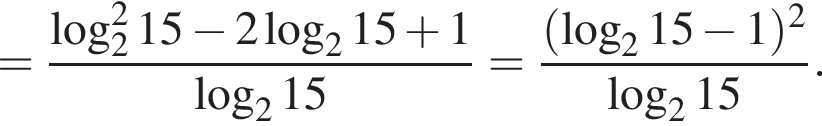
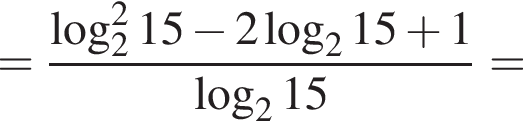
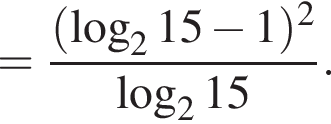
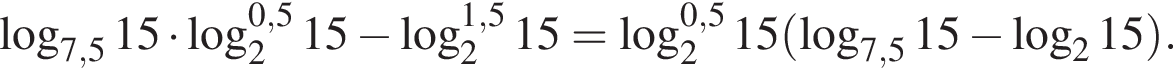
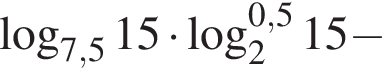
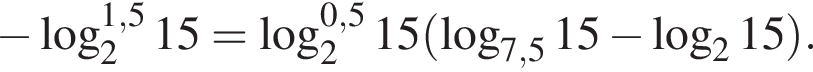
 Тогда имеем:
Тогда имеем: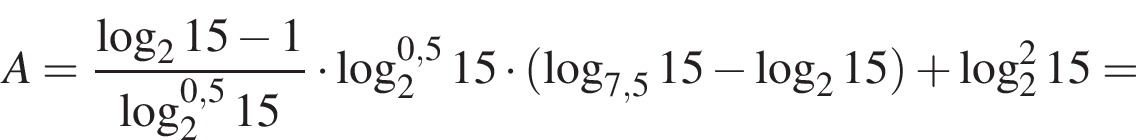
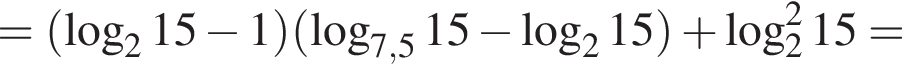
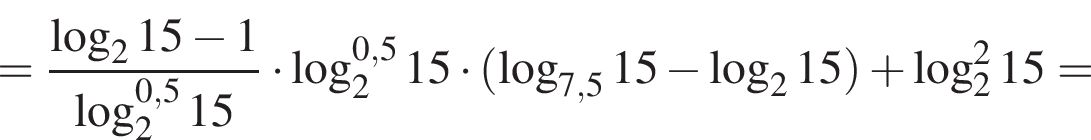
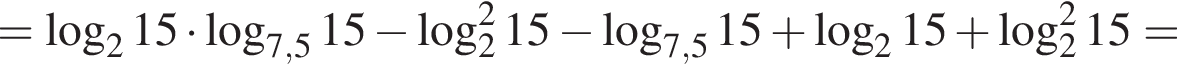
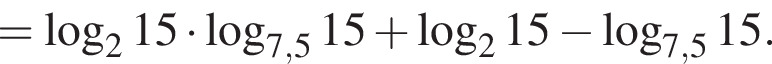
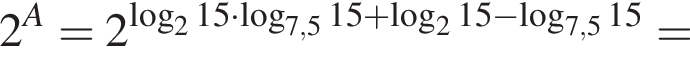
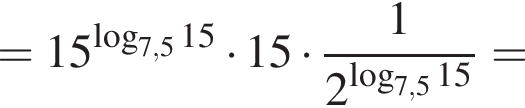
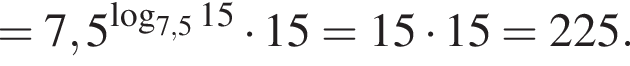
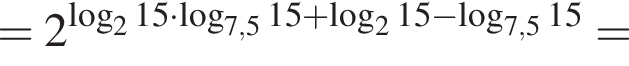
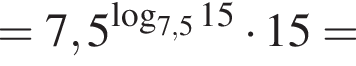
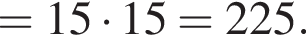
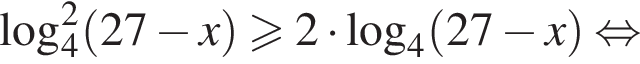
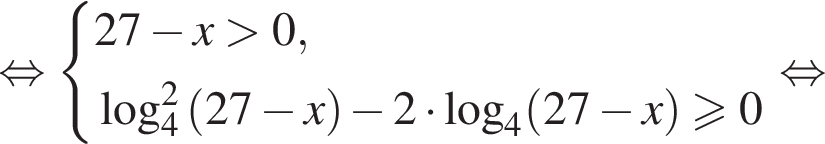
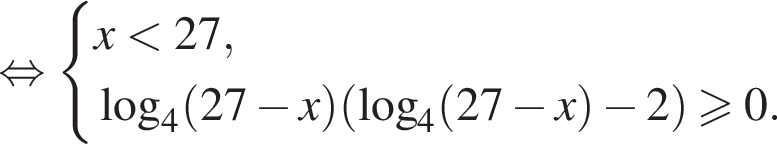

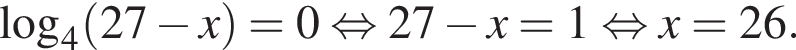
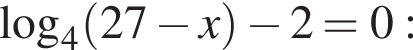

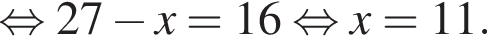
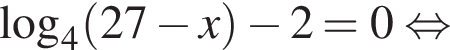
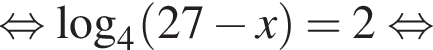
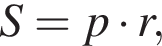 где p — полупериметр. Находим:
где p — полупериметр. Находим: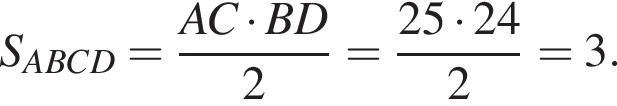
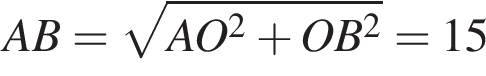 и
и 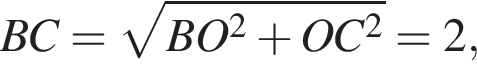 следовательно,
следовательно,